[번역] 헬름홀츠-엘리스 기보법 입문편

 

헬름홀츠-엘리스 기보법

이 콘텐츠는 일본어 원문 ( https://note.com/nayuta_823543/n/n2799686376d3 )의 한국어 번역입니다.

 

안녕하십니까, 유토피아! 変拍子兄さん의 시간이 왔습니다.

 

오늘은 미분음 초심자를 위해서 헬름홀츠-엘리스 기보법이라는, 올림표·내림표보다 더욱 세밀한 기호들에 대해서 이야기해보도록 하겠습니다.

 

이전에도 소개한 적이 있는 기호이지만, 수학 관련 이야기를 제외하고 하겠습니다.

 

 

 

지금까지 12평균율이라는 모습으로 간략화된 음정을 사용해왔습니다.

 

이것과는 달리, 미분음이라는 것은 더욱 세밀하게 접근하자는 느낌이기에, 12평균율보다는 난이도가 올라가게 되지만, 어쩔 수가 없습니다.

 

 

 

그래서, 12평균율밖에 모르는 상태에서, 헬름홀츠-엘리스 기보법과 만나게 되었을 경우, 어떻게 대처해야 좋을까에 대해 해설해보도록 하겠습니다.

 

---

 

《목차》

 

• 헬름홀츠-엘리스 기보법은 어떤 기호인가
• 센트는 사용하지 않는다
• 2등분편
• 3등분편
• 5등분편
• 보다 더욱 세밀한 기호들
• 평균음정용 기호
• 마치며

 

---

 

헬름홀츠-엘리스 기보법은 어떤 기호인가

 

먼저, 헬름홀츠-엘리스 기보법은 어떤 것일까요? 잠깐 공식 문서를 읽어봅시다.

 

준비되셨습니까?

 

http://www.marcsabat.com/pdfs/notation.pdf

 

공식 문서 일부 발췌

 

네, 척 봐도 어려워 보입니다.

 

링크에 있는 PDF에 자세하게 쓰여있습니다만, 정말로 어렵기 때문에, 흘끗 보는 것만으로 만족합시다.

 

그리고 이 기호를 붙이게 되면 어느 정도 음정이 변할까에 대한 것은 다음 웹 어플리케이션을 이용하면 알 수 있습니다.

 

https://www.plainsound.org/HEJI/

 

페이지를 들어가자마자 조우할 수 있는 경악스러운 기호의 나열이다.

 

그러나, 이것도 종류가 다양해서 알기 어렵네요. 다만 기억해 두었으면 하는 부분은 몇 개든 늘어 놓아도 OK라는 것입니다. (덧붙여 모두 늘여놓는 것도 가능합니다.)

 

 

 

 

 

음식점에서 이렇게 추가주문을 한다면, 아마 어디의 뭐하는 사람인지 확인하러 나올 것이다.

 

 

 

 

이 웹 어플리케이션을 이용하는 법은 잠시 뒤로 미뤄두고, 지금은 여기에 나오는 기호를 해설하도록 하겠습니다.

 

지금 하는 것만으로도 충분히 많은 양이지만, 실제로는 더욱더 많이 있습니다.

 

힌트라면은, 이 오른쪽 열의 숫자의 나열에 관해서 말 입니다만, 소수가 주르륵…….이라는 것으로 '이 뒤로도 계속 있구나~'라는 것을 상상해주셨으면 합니다.

 

소수가 주루룩 놓여있다.

 

 

센트는 사용하지 않는다

 

미분음 관련 얘기에서 항상 등장하는 '센트(cent)'.

 

반음을 100등분한 단위입니다만, 이번에는 봉인하도록 하겠습니다.

 

머릿속에 상상해 주었으면 하는 것은 피아노의 12음. 그리고 그것을 몇 등분할까라는 생각. 그것 정도면 충분합니다.

 

 

 

욕심을 부리자면, 배음의 존재에 대해서도 파악해 주셨었으면 하는 바이지만, 이번에는 그런 것도 있구나 하는 정도로 OK입니다.

 

 

 

실제로, 이거는 551센트다! 하는 것보다, 대략 F랑 F#의 중간 즈음이라고 하는 것 정도로도 충분하니까요.

 

 

 

그리고 '사이'라는 것은 2등분에 기반한 생각.

 

이것을 3등분, 4등분, 5등분……으로 늘려보겠습니다.

 

센트로 표현하면 엄밀히 비교가 편하게 되지만, 그것은 너무 세밀하기 때문에 패스하겠습니다.

 

 

 

정말 정확히 딱 맞아떨어지는 3등분 같은 것이 아니다는 약간 유도리가 존재하는 개념이라고 생각하시면서 계속 읽어주세요.

 

그렇기 때문에, 기호끼리의 합(덧셈)은 기본적으로 불가능하다고 생각해주세요.

 

 

 

2등분편

 

그건 그렇고, 혹시 이렇게 생긴 기호가 나온다면, 어떻게 할까요?

 

#에서 선을 몇 개 빼버린 듯한 이 십 자(十) 모양의 기호 말입니다.

 

 

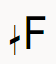
F 기준으로 어느 정도 높이거나 낮추는 건가?라고 생각합니다만,

 

이것이 반음을 2등분한 만큼 올리는 기호입니다. 다시 한번 짚자면 '대체적으로 이 값'이라는 말입니다.

 

 

 

그러면, 낮추는 쪽은 어떻게 하지?라는 질문에, 이 모양을 보여드릴 수 있습니다. 좌우가 뒤집힌 ♭기호입니다.

 

 

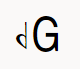
이 쪽은 반음을 2등분한 만큼 내리는 기호 정도로 충분합니다.

 

 

 

그리고 밑의 '부등호 > 모양에 봉이 꽂혀있는 기호' 또한 반음을 2등분한 만큼 올리는 기호입니다.

 

 

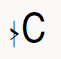
그리고 각진 q처럼 생긴 기호 또한 반음을 2등분한 만큼 내리는 기호입니다.

 

 

반음을 2등분하여 이용하는 기호가 2종류가 있다니, 복잡하군요.

 

실제로는 약간 음정의 폭이 다르기 때문에, 다른 기호입니다.

 

뭐, 급격하게 파고들게 되기 때문에, 크게 신경 쓰지 않아도 좋습니다.

 

 

 

덧붙여, 이 반음을 2등분하여 이용하는 기호를 여러 개 사용한다고 해도, #이나 ♭가 되느냐 라고 물으신다면, 엄밀히 말해서 안 됩니다.

 

그렇기 때문에 기호가 2개 있다고 치환하거나 해버리면 안됩니다.

 

 

 

3등분편

 

조금 어려워집니다만, 반음을 3등분한 것을 상상해봅시다.

 

미부터 파까지 미→○ →○ →파라는 느낌으로, 사이에 2단계의 음정을 상상할 수 있다면 좋습니다.

 

 

 

그러면, 본론으로 넘어가서, 이 기호는 반음을 3등분한 만큼 올리는 기호입니다.

 

7을 뒤집은 모양을 하고 있습니다.

 

그리고 이쪽이 반음을 3등분한 만큼 내리는 기호입니다.

 

L 모양 같습니다.

 

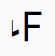
아까 전의 기호와는 다르게, 모양이 정확히 상하 반전된 것을 알 수 있습니다.

 

이 기호는 이중으로 결합할 경우, 다음과 같이 결합됩니다.

 

 

 

 

 

다음으로, 조금 어려울지도 모릅니다만, 온음을 3 등분한다고 상상해 봅시다.

 

도부터 레까지 도 →○ →○ →레라는 느낌으로, 사이에 2단계의 음정을 상상할 수 있다면 좋습니다.

 

반음의 2/3이라는 느낌도 가능합니다.

 

 

 

그러면 재빨리 본론으로 넘어가겠습니다.

 

이 기호는 온음을 3등분한 만큼 올리는 기호입니다.

 

＃에서 가로선 하나를 뺀 것 같은 모양입니다.

 

그리고 이 밑의 기호가 온음을 3등분한 만큼 내리는 기호입니다.

 

♭를 뒤집고, 세로선을 하나 더 그려준 것 같습니다.

 

 

 

이것도 '반음 3등분한 기호가 2개 있으면, 온음 3등분 기호 하나로 바꿔도 되는가'라고 하면,

 

크게 보면 얼추 맞습니다만, 엄밀히 따지면 옳지 않습니다.

 

 

 

 

5등분편

 

더욱 상상하기 어렵습니다만, 반음의 5등분이 등장했습니다.

 

이것 또한, 미부터 파까지 미 →○ →○ →○ →○ → 파라는 느낌으로 상상할 수 있다면 좋습니다.

 

 

 

어렵다면, 4등분을 생각하여도, 큰 차이는 없습니다.

 

재빠르게 넘어가 봅시다.

 

이것은 ♮ 에 화살표가 붙어 있습니다. 반음을 5등분한 만큼 올리는 기호입니다.

 

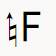
이 기호는 종속성이 있기 때문에, 다른 기호에 기생하는 형식으로도 나타납니다.

 

그렇다 하여도, 일부 기호에만 기생이 가능하기 때문에, 기호라고 해서 아무렇게나 붙어대는 것은 아닙니다.

 

그렇기 때문에, 다른 기호들과 조합하는 경우, ♮ 에 붙는 모습을 자주 씁니다.

 

 

 

물론, 반음을 5등분한 만큼 내리는 기호 역시 존재합니다. 

 

상하 방향 화살표이기 때문에, 알기 쉽네요.

 

 

 

 

 

보다 더욱 세밀한 기호들

 

자, 다음은 더욱 세밀한 기호들입니다.

 

 

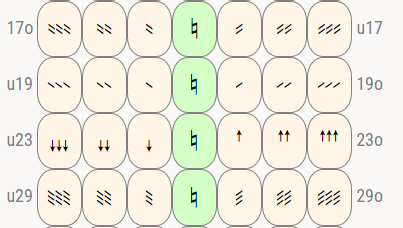
이렇게까지 세밀하면, 센트로 얘기하는 쪽이 더욱 알기 쉽지만, 일단 몇 등분이냐에 관해서 적자면,

 

 

 

반음의 6등분

 

반음의 9등분

 

반음의 15등분

 

반음의 30등분

이렇게 됩니다. 

 

헬름홀츠-엘리스 기보법을 사용할 때, 악보의 기본값이 12평균율이 아니게 되어버리기 때문에,

 

이 단계까지 세밀하게 하게 된다면, 엄밀하게 다룰 필요가 있습니다.

 

즉, 이 정도 부근부터는 '대충 몇 등분'같은 방법이 통용되지 않는다는 것입니다.

 

 

 

자세히 알고 싶다!라고 하시는 분은, 부디 미분음이라는 늪에 한 발자국 더 깊이 발을 들여놓아 보시는 것은 어떻겠습니까?

 

 

평균음정용 기호

 

참고로, 헬름홀츠-엘리스 기보법은, 밑과 같이 머리에 선을 그은 타입의 기호가 있습니다.

 

이것은, 딱 음정을 몇 등분할까 하는 때에 이 선을 붙입니다.

 

이번 이야기는 '대략적으로' 이해할 수 있는 정도 선에서 충분합니다만,

 

엄밀히 몇 등분이고 뭐고 하는 경우에는 이렇게 가로선을 머리에 붙여줄 필요가 있습니다.

 

 

 

이것 또한, 깊게 들어가면 어려운 부분이 되기 때문에, 입문으로서는 소개 정도만 하는 것으로 해두겠습니다.

 

 

 

마치며

 

이렇게 해서, 이번에 나온 기호들을 정리해 보았습니다.

 

이렇게 해서, 헬름홀츠-엘리스 기보법에 대해서 대략적으로 알아보았습니다.

 

이런 세세한 기호를 사용해서 무엇을 하고 싶은 것인가?라는 이야기가 됩니다만,

 

세세한 기호의 존재 의의는 배음을 다루기 위한 목적입니다.

 

 

 

그 말인즉슨, 헬름홀츠-엘리스 기보법을 사용하면, 배음과 순정음정을 딱 맞춰 지정할 수 있습니다. 

 

그렇기 때문에, 엄밀히 다루기 위해서는, 센트와 대수, 피타고라스 음률, 몬조 같은 수학적인 지식을 몸에 익힐 필요가 있습니다.

 

이번에는 헬름홀츠-엘리스 기보법의 아주 미약한 발걸음이었습니다. 헬름홀츠-엘리스 기보법의 깊은 늪에 들어가기 위해서는, 그만큼의 지식을 장비하고 돌격해 주시기 바랍니다.

 

 

 

이번에는 입문편이기 때문에, 직관적으로 사용하기 위해서는 이번 같은 대략적인 것에 대한 이해 정도로 문제없습니다. 

 

배음에 맞춰서 사용한다는 본래의 의미를 알고 싶으셨다면, 죄송합니다만, 이번엔 패스하도록 하겠습니다. 

 

이렇게 해서, 헬름홀츠-엘리스 기보법 입문편이었습니다.

 

---

궁금한 점이 있으시면, 이 글의 댓글로 자유롭게 물어보십시오.